Trigonometrie, also Dreiecksberechnung ist ein sehr wichtiger Teil
der Programmierung. Es dient zum berechnen von Entfernungen,
Sichtbarkeiten, zum Erstellen von Kurven und vielem mehr - kurzum
ohne Dreiecksberechnungen kommt man nicht sehr weit.
Ziel der Berechnungen ist es, immer fehlende Stücke aus den bereits
Bekannten zu ermitteln.
Am einfachsten und häufigsten benötigt sind diese Berechnungen im
rechtwinkligen Dreieck.
|
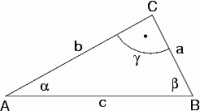
Ein Dreieck besteht ja aus 3 Seiten und 3 (Innen)Winkeln.
Die längste Seite ,also auch die, die dem größten Winkel
gegenüberliegt (im rechtwinkligen Dreieck ist dies der rechte
Winkel) ist die Hypotenuse. Die beiden anderen Seiten bezeichnet
man als Katheten.
|
 |
So, das hilft uns allerdings noch nicht viel weiter. Um etwas
ausrechnen zu können, brauchen wir erst die Winkelfunktionen.
Sie heißen Sinus, Cosinus und Tangens. Sie sind wie folgt definiert:
Sinus(winkel) = Gegenkathete/Hypotenuse
Cosinus(winkel) = Ankathete/Hypotenuse
Tangens(winkel) = Gegenkathete/Ankathete
Die Gegenkathete ist immer die Kathete, die einem Winkel gegenüberliegt,
die Ankathete dementsprechend die, die direkt am Winkel liegt.
Wenn man diese kleinen Funktionen jeweils nach der gesuchten
Größe umstellt, kann man damit praktisch schon alles im (rechtwinkligen!)
Dreieck ausrechnen.
Hilfreich ist noch der berühmte "Satz des Pythagoras", über den man
eine dritte Seite im Dreieck ausrechnen kann, wenn die 2 anderen gegeben
sind. Er lautet a²+b²=c², wobei c die Hypotenuse und a und b die Katheten sind.
Diesen Satz des Pythagoras muss man dann nurnoch nach der gesuchten Seite
umstellen und voilá :-)
Da man in der Praxis aber nicht immer rechtwinklige Dreiecke vorfindet,
kommen wir jetzt zu den beliebigen Dreiecken und deren Berechnung.
Wichtig ist da als erstes der Sinussatz. Der lautet wie folgt:
a/sin(alpha) = b/sin(beta) = c/sin(gamma)
Oder umgekehrt (so kann man leichter nach Winkelgrößen umstellen):
sin(alpha)/a = sin(beta)/b = sin(gamma)/c
Dann gibts noch den Cosinussatz. Der ist da schon etwas kompliztierter:
a²=b²+c²-2bc*cos(alpha)
b²=a²+c²-2ac*cos(beta)
c²=a²+b²-2ab*cos(gamma)
Lässt sich aber im Grunde auch relativ einfach umstellen.
Zu guter letzt sollte man noch wissen, dass die Innenwinkelsumme in einem
Dreieck immer 180° ergibt - so kann man leicht einen dritten Winkel
ausrechnen, wenn die anderen 2 gegeben sind.
So, nach dieser trockenen Theorie wollen wir jetzt mal 2 kleine Programme
schreiben die die Anwendung zeigen. Als erstes wollen wir die berühmten
Sinuskurven nachbilden.
Dazu nehmen wir ein Grundgerüst, wie wir es schon 100 mal genutzt haben:
|
|
Graphics 1024,768,16,1
SetBuffer BackBuffer()
While Not KeyDown(1)
;blabla
Flip
Cls
Wend
|
Und wollen nun ein Quadrat von oben nach unten in einer Kurve fliegen lassen.
Dazu vergrößert sich y Linear und wenn es die maximale Auflösung überschreitet
soll es wieder aus 0 springen, also:
|
|
y = y + 1
If y = 768 Then y = 0
|
Dann lassen wir x als Sinuswert von y berechnen, setzen es in die Bildmitte
und Multiplizieren es noch etwas, damit wir überhaupt was sehen (Sinuswerte
können nur Werte zw. -1 und 1 annehmen):
Erweitert um ein 2. Quadrat, dass eine etwas schwächere Kurve fliegt,
könnte das dann so aussehen:
|
|
Graphics 800,600,16,2
SetBuffer BackBuffer()
While Not KeyDown(1)
y = y + 1
If y = 600 Then y = 0
x = 400+Sin(y)*50
x2 = 400+Sin(y)*25
Color 255,128,64
Rect x,y,10,10
Color 200,100,40
Rect x2,y-50,10,10
Flip
Cls
Wend
|
Die Flugbahn kann man ganz einfach nachverfolgen, wenn man das Cls entfernt.
Wie man sieht, ist es also ziemlich einfach.
|
Und nun zum zweiten Programm. Wir wollen versuchen, ein Programm zu schreiben
dass beliebige, regelmäßige Vielecke erzeugen kann.
|
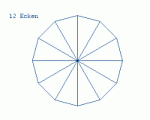 |
Im Grunde ist so ein "beliebiges, regelmäßiges Vieleck" ja ziemlich einfach
aufgebaut.
360°/Anzahl_der_Ecken ergibt z.B die Gradzahl für jedes Dreieck
aus dem das Vieleck aufgebaut ist. Die Funktion die das Vieleck zeichnet
zerlegt die Zeichnet nur rechtwinklige Dreiecke und zeichnet diese dann
ein (rechtw. Dreiecke lassen sich schön einfach einzeichnen..)
Zusammen mit einigen grafischen Finessen (puh, schreibt man das so?) ergibt sich so
ein Programm:
|
|
Graphics 640,480,16,1
SetBuffer BackBuffer()
radius = 200
neueecke = 1
maxecken = 32
While Not KeyDown(1)
ecken = ecken+neueecke
If ecken = maxecken Or ecken = 0 Then neueecke=-neueecke
radius = ecken*4+50
vieleck(ecken,radius,GraphicsWidth()/2,GraphicsHeight()/2)
Text 10,10,ecken+" Ecken"
Flip
Cls
Delay 100
Wend
;---------------------------------------------------
Function vieleck(ecken,radius,mittelpx,mittelpy)
b = radius
For ecke = 1 To ecken
alpha# = 360.0/ecken*ecke
Xalpha# = 360.0/ecken*(ecke-1)
gamma# = 90-alpha#:
Xgamma# = 90-Xalpha#
h# = b*Sin(alpha#): Xh# = b*Sin(Xalpha#)
c# = b*Sin(gamma#): Xc# = b*Sin(Xgamma#)
Color 255,ecke*2,ecke*8
Line mittelpx,mittelpy,mittelpx+c#,mittelpy+h#
Line mittelpx+Xc#,mittelpy+Xh#,mittelpx+c#,mittelpy+h#
Next
End Function
|
Wo man Dreiecksberechnungen noch anwenden kann? Stellen Sie sich z.B ein 2D-Spiel in der
Draufsicht vor. Vorher sollen die Gegner wissen, ob sie den Spieler sehen oder nicht?
Ganz einfach - man bildet ein Dreieck für den Sichtkegel und schaut ob der Spieler da
drin ist oder nicht. Oder wie lenkt man z.B in einem 3D-Weltraumballerspiel aus Egosicht
die Schüsse zum Fadenkreuz? Richtig - per Dreiecksberechnung.
|
|